Vickrey auction に見る incentive compatibility

タイトルからは小難しそうな感が漂っていますが、見かけ倒しです。

0. 目次

はじめに
incentive compatibility
simplified Vickrey auction
おまけ：Vickrey auction on Blockchain
次回予告
参考文献

1. はじめに

気が変わらなければ、次回は、メカニズムデザインにおいて重要な概念である incentive compatibility について、具体的な事例を交えながら整理する予定です。cryptoeconomics というよりは、まずはその土台となるミクロ経済学（市場理論、ゲーム理論、メカニズムデザインなど）に寄り添っていこうというスタンスです。

と書きましたが、気が変わらなかったので、この通りの内容でいこうと思います。ここで言っている「具体的な事例」としては、記事タイトルにもある通り、簡単化した Vickrey auction を用います。Vickrey auction については以前の記事でもさらりと触れましたが、今回はもっとわかりやすく具体的な説明を試みます。

2. incentive compatibility

まず、そもそも incentive compatibility（誘因両立性）ってなんぞや？という方も多いと思うので、これについて軽く説明したいと思います（よりフォーマルな定義については今後のアウトプットの中で突っ込んでいければと思います）。

まずは Wikipedia さんから概要を引用します。

A mechanism is called incentive-compatible (IC) if every participant can achieve the best outcome to him/herself just by acting according to his/her true preferences.

訳してみます。

全ての参加者が自身の真の選好に従って行動するだけで利得を最大化できるとき、そのメカニズムを incentive compatible（IC）と呼ぶ

こんな感じでしょうか。噛み砕くと、

incentive compatible なゲームルール：正直者が一番得するようなゲームルール

ということです。で、「正直者が一番得するような」性質そのものが incentive compatibility、というわけです。

そもそも、メカニズム（政策など）を実装する側が各プレイヤーの選好（個人情報）を正確に把握することは極めて困難です。全プレイヤーに対して愚直に「あなたの選好を教えてください」と尋ねて回って最適なメカニズムをつくろうとしても、プレイヤーからすれば、真の選好を教えること自体が得策ではないかもしれません。ということで、わざわざ選好を把握せずとも、各プレイヤーが正直に自身の選好に従うことで一番得をするような仕組みがつくれたら、それは非常に実用的だと考えられます。

と、こんな感じで、メカニズムデザインにおいては incentive compatibility が重要視されているわけです。

また、incentive compatibility にもいくつか種類があり、その中の 1 つとして、strategyproofness（耐戦略性）があります。経済学関連の文献を読んでいると、こっちを見かけることの方が多かったように思いますし、厳密には Vickrey auction はこれを満たすメカニズムなので、概要を掴んでおこうと思います。

先ほど引用した Wikipedia の記述のすぐ下に以下のような記載があります。

The stronger degree is dominant-strategy incentive-compatibility (DSIC). It means that truth-telling is a weakly-dominant strategy, i.e you fare best or at least not worse by being truthful, regardless of what the others do. In a DSIC mechanism, strategic considerations cannot help any agent achieve better outcomes than the truth; hence, such mechanisms are also called strategyproof or truthful.

訳してみます。

強い incentive compatibility が dominant strategy incentive compatibility（DSIC）。これは、「本当のことを言うことが弱支配戦略である」ということを意味する。すなわち、「他のプレイヤーの行動に関わらず、正直であれば、その他の戦略と同等以上の利得が得られる」という性質である。DSIC メカニズムにおいては、どんなプレイヤーも「戦略的配慮を行うこと」によって「正直であること」よりも大きな利得を達成することはできない。したがって、このようなメカニズムは strategyproof もしくは truthful とも呼ばれる。

ちょっと意訳が多いですが、こんな感じでしょうか。「耐戦略」というのは、「あれこれ考えて戦略立てても意味ないよ」ということを意味するのでしょう。

さて。今回の目的は Vickrey auction の仕組みを通じて、incentive compatibility（厳密には strategyproofness）を「より直感的に」理解することなので、小難しい文章と戯れるのはここまでにして、早速、具体的な Vickrey auction の話に移ります。

3. simplified Vickrey auction

今回は、簡単化した Vickrey auction を用いて解説します。まず、そのルールについて説明します。

登場人物はアリスとボブの 2 人です。2 人は商品（クマさん）に対して入札額を決め、入札します。そして、入札額が高かった方が落札します。と、これだけ聞くと、一般的なファーストプライス・オークションと同じように思えますが、Vickrey auction では、これに加えて、さらに以下のようなルールが追加されます。

開票時まで、入札額は他の入札者に対して公開されない（封印入札型）
落札者が実際に支払う金額は、二番目に高い入札額（セカンドプライス・オークション）

また、今回は簡単化のため、アリスとボブは入札額を以下から 1 つ選んで入札することとします。

1 ETH
2 ETH
3 ETH
4 ETH
5 ETH

アリスとボブの入札額が同じだった場合は、くじ引きを行うこととします。くじは、アリスが当選する確率もボブが当選する確率も等しく 1/2 であるとし、当選した方が入札額を支払って商品を落札することとします。

ルールはこれだけなので、早速、このルールが strategyproofness を満たしているのか考えてみます。

今回は、アリスの立場に立って考えてみます。仮に、アリスが

「あのクマさんになら 3 ETH 支払ってもいいワ」

と思った場合、いくらで入札するのがよいでしょうか？

まず、いくつかのパターンをピックアップし、それぞれのパターンにおいてアリスがどれだけ得をするのか（アリスの利得）について考えてみます。

アリス：3 ETH 　 vs.　ボブ：2 ETH
- 結果：アリスが 2 ETH で落札
- 利得：1 ETH（3 ETH と評価していたものを 2 ETH で落札できた）
アリス：5 ETH 　 vs.　ボブ：4 ETH
- 結果：アリスが 4 ETH で落札
- 利得：-1 ETH（3 ETH と評価していたものを 4 ETH で落札してしまった）
アリス：3 ETH 　 vs.　ボブ：4 ETH
- 結果：ボブが 3 ETH で落札
- 利得：0 ETH（所持 ETH に変動はないので、損も得もなし）
アリス：2 ETH 　 vs.　ボブ：2 ETH
- 結果：くじ引きで当選した方が 2 ETH で落札
- 利得（期待値）：0.5 ETH（ 1/2 の確率で利得 1 ETH、 1/2 の確率で利得 0 ETH）

さて。利得の計算方法はイメージできたと思うので、全てのパターンにおけるアリスの利得を表で整理してみます。

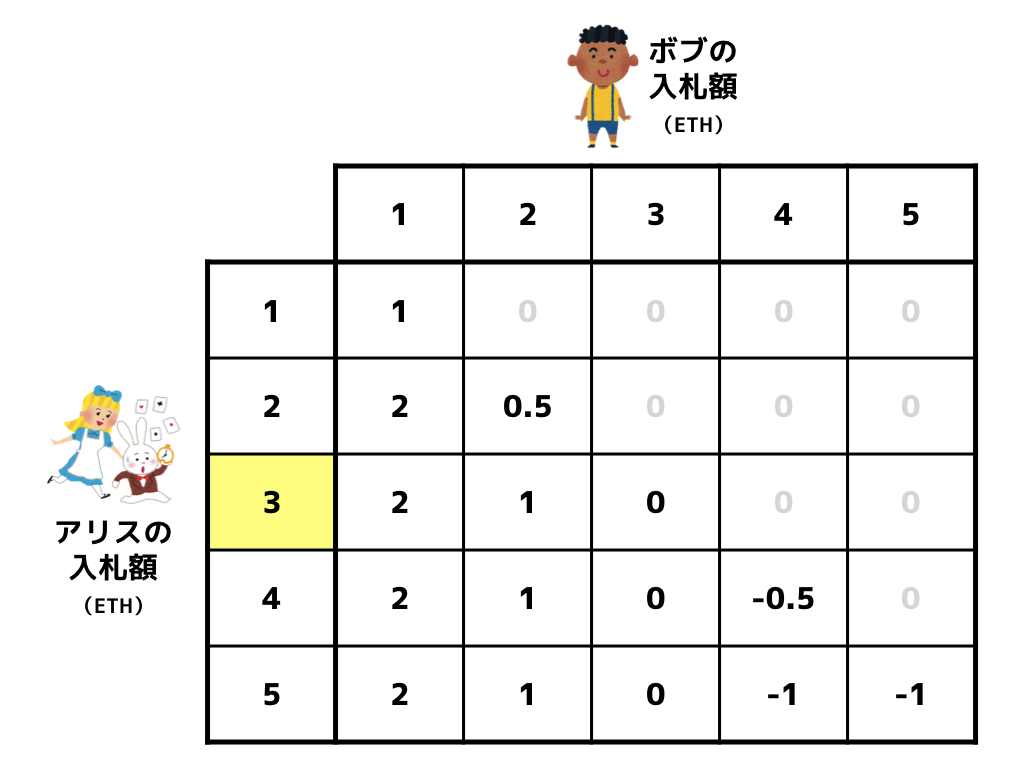
この表を見ながら、「あのクマさんになら 3 ETH 支払ってもいいワ」と考えているアリスが、いくらで入札すべきなのか考えてみます。ここで注意すべきは、ボブがいくらで入札してくるのかはまったく分からないということです。

まず、2 ETH で入札するときと 3 ETH で入札するときを比べてみます。

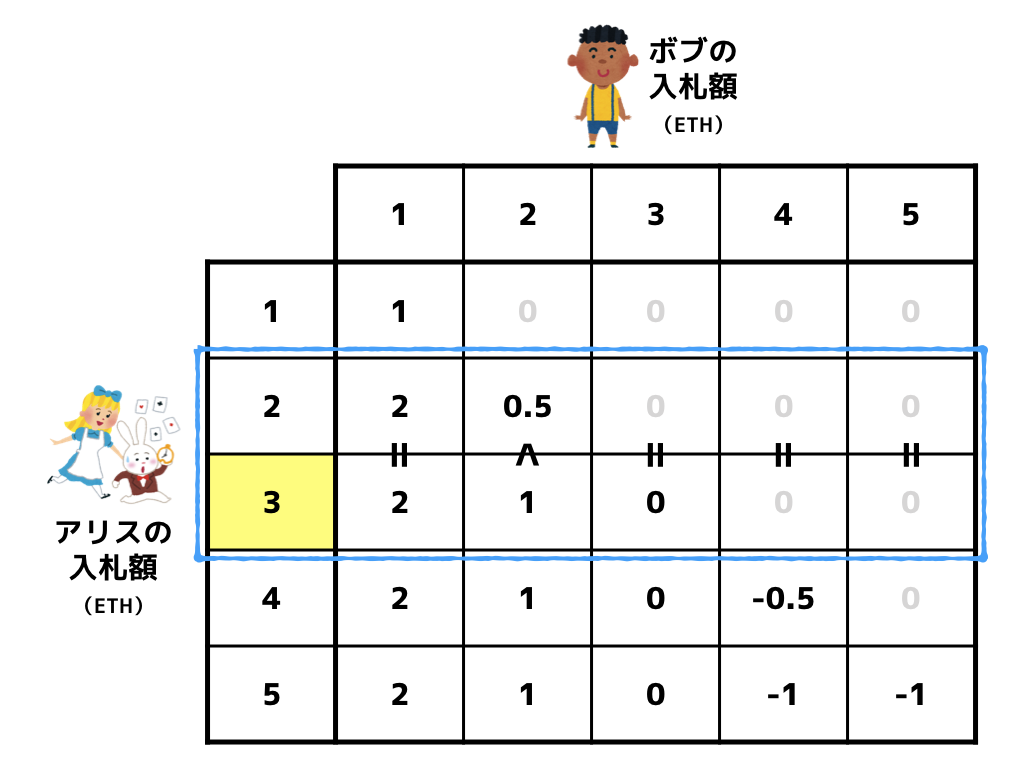
ボブの入札額が 1 ETH or 3 ETH or 4 ETH or 5 ETH の場合、アリスは 2 ETH で入札しようが 3 ETH で入札しようが利得は変わりません。しかし、ボブの入札額が 2 ETH の場合、アリスは 2 ETH で入札するよりも 3 ETH で入札するときの方が利得が大きくなります。よって、アリスは 2 ETH で入札するよりも 3 ETH で入札すべきでしょう。

次に、3 ETH で入札するときと 4 ETH で入札するときを比べてみます。

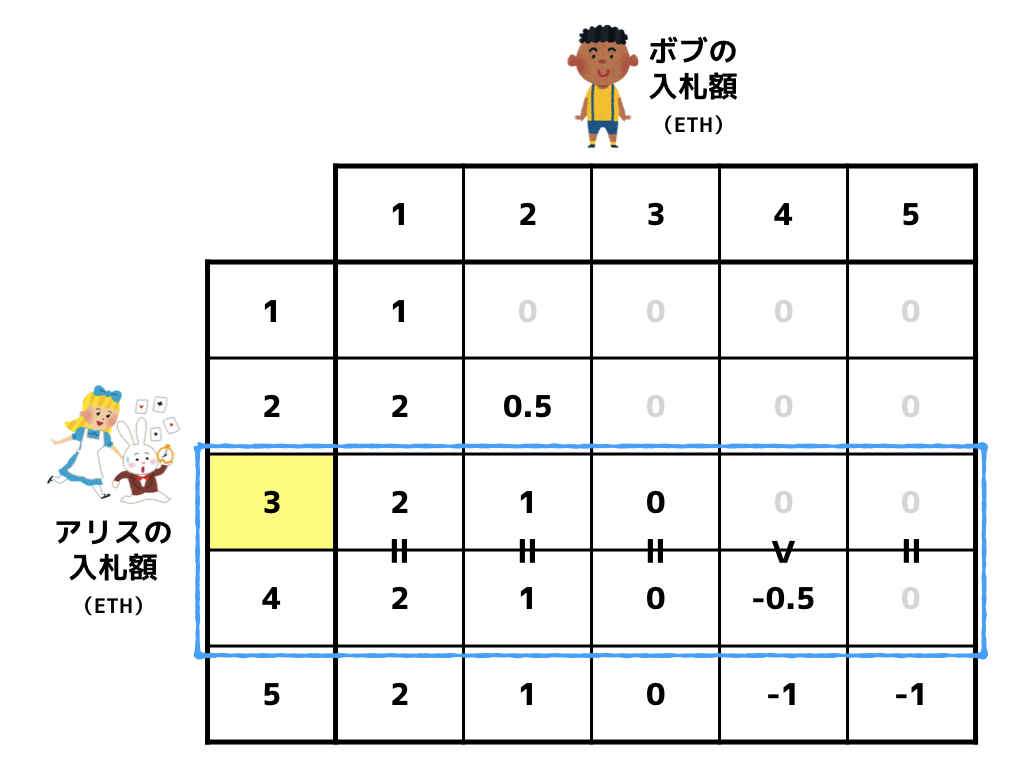
ボブの入札額が 1 ETH or 2 ETH or 3 ETH or 5 ETH の場合、アリスは 3 ETH で入札しようが 4 ETH で入札しようが利得は変わりません。しかし、ボブの入札額が 4 ETH の場合、アリスは 4 ETH で入札するよりも 3 ETH で入札するときの方が利得が大きくなります。よって、アリスは 4 ETH で入札するよりも 3 ETH で入札すべきでしょう。

また、同様に考えると、1 ETH で入札するよりも 3 ETH で入札すべきであり、5 ETH で入札するよりも 3 ETH で入札すべきであることが分かります。

これらを加味すると、

アリスは「あのクマさんになら 3 ETH 支払ってもいいワ」という自分の気持ちに正直に 3 ETH で入札するのが最も合理的

ということになります。もちろん、評価額が 3 ETH でないときも、評価額を正直に入札するのが最も合理的となります。また、アリスもボブも状況は同じなので、ボブの立場に立って考えてみても同じことです。

以上、（簡単化はしていますが）Vickrey auction を通じて、「正直者が一番得するようなルールになっている（前述した strategyproofness を満たしている）」とはどういうことかを理解していただけたかと思います。

4. おまけ：Vickrey auction on Blockchain

せっかくなので、Vickrey auction をブロックチェーン上で（例えば、Ethereum のスマートコントラクトで）実装することについても検討してみます。

例えば以下のような方針であれば、実装すること自体は可能なように思えます。

商品は ERC20 トークンや ERC721 トークン
封印入札（と開票）に関しては、commit-reveal voting のような手法を採用する
セカンドプライス・オークションに関しては、素直にそういうコントラクトを書く

実際、Solidity での実装例も公開されています。

しかし、Vitalik もこのスライドの中で提起しているように、複数入札が問題となります。もし、入札コストが十分に小さいのであれば、以下のようなハックが簡単にできてしまうというわけです。

複数のアドレスを用意する（スマートコントラクトに「1 アドレス 1 入札」などの制約があっても回避）
複数のアドレスから様々な入札額で入札する
他の入札者の開票状況を観測しながら、都合のよい入札だけを開票する

このハックを妨げるためには、

入札と同時に入札額以上のデポジットを要求し、入札額以上のデポジットがなければ開票できないようにする
開票期間に開票されなかった入札については、デポジットを回収できないようにする

という対策が思い浮かびます。し、そもそも入札額分の資金を保有していることを証明するためにも、これは妥当な仕様だと考えられます。実際、先ほど引用した実装例も同様の手法を採用しています。

しかし、この手法だとデポジット額は公開されてしまうため、他の参加者の入札額をある程度予想することが可能となってしまいます。すなわち、完全な封印入札ではなくなり、incentive compatibility が失われてしまいます。また、これで複数入札ハックが完全に防げるわけでもないです（どうしても落札したければ、開票しない入札が生じるのを覚悟で複数入札することはできます）。

これに対して、Vitalik は、以下のようなソリューションも提案しています。

入札額に上乗せした分のデポジット量を基準にしてオークション売上の一部を分配する
偽入札（落札額には到底及ばないような入札額だが、デポジット額は非常に大きいような入札）を奨励する

これらがうまく機能すれば、入札状況の予想がより困難となり、「実質的な封印入札」が実現されるということでしょう。とはいえ、実際にこれらのソリューションがうまく機能する確証はありません。これらがうまく機能することを示すためには、形式的にモデル化し、よりアカデミックに議論する必要があるでしょう。

このように、理論的には画期的なメカニズムがあったとしても、理想的な性質を保ったまま分散型の世界で機能させることは予想以上に難しいわけです。裏を返せば、この難しさが cryptoeconomics を新しい学問足らしめているとも言えるのではないでしょうか。

5. 次回予告

実は、今回取り上げた Vickrey auction は、グローヴスメカニズムと呼ばれるメカニズムの一例に過ぎません。すなわち、より抽象的なグローヴスメカニズムというスキームを理解することで、Vickrey auction のような strategyproofness を満たした別のゲームを設計できるというわけです。凄いですね。ということで、次回以降は、

グローヴスメカニズムについて形式的に（数式レベルで）整理する
実際に VCG メカニズムから Vickrey auction を導出する

あたりにチャレンジしていければなと考えています。